Изобарный процесс: формулы, графики, уравнения
Изобарный (или изобарический) процесс — физическое воздействие, которое происходит при постоянной тяжести вещества в газовом состоянии, а также при неизменности показателя давления. Также возможно определить изобарный процесс в качестве процедуры трансформации газообразного вещества идеального типа в иной вид состояния, причем не должно наблюдаться изменение показателей давления. Изобарный процесс является одним из основных в термодинамике.
Изначально данный процесс в физике был исследован ученый французского происхождения Жозеф-Луи Гей-Люссак. В честь этого ученого был назван физический закон, описывающий все изотермические процессы.
Посмотрим, как работает данный физический закон — изначально необходимо прописать базовое выражение для этого закона: ([Ptimes=vtimestimes]) . Далее необходимо прописать те величины, которые остаются неизменными: v=const, P=const. В таком случае получается следующее соотношение: ([frac>>=frac>>]=…) Причем это соотношение будет верно для всех газовых состояний. Получается, что ([frac=const]) . Это и есть теорема Гей-Люссака.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Данный закон показывает, насколько коррелирует, какие тесные взаимодействия существуют между объемом и температурными показателями. Если происходит возрастание температурных показателей, тогда происходит и возрастание объемов. Также если уменьшается температура, тогда пропорционально уменьшается и объем.
Количество теплоты, которое выделяется при изобарном процессе, значительно превышает количество теплоты, которое выделяется при изохорном процессе, причем при условии неизменности объема. В настоящих газовых веществах некоторая доля теплоты тратится на преобразование усредненного количества энергии кооперации газовых частиц. Система в изобарном типе процесса при учете числа теплоты производит работу, то есть не происходит только нагрев. Количество работы, которое производится идеальным типом газового вещества при изобарном процессе эквивалентно pdV. В данном выражении p является показателем давления, dV является показателем перемены объемов.
Условия протекания изобарного процесса
Для того, чтобы производить изобарный процесс, необходимо к месту эксперимента подключать теплоту или же отключать подачу тепла. Теплота используется для того, чтобы совершить работу преобразования и расширения энергии внутри системы.
Кто открыл
Как уже было сказано выше, открыл данный закон Жозеф Луи Гей-Люссак. Это ученый в области физики и химии французского происхождения, он также являлся представителем Французской Академии наук в начале 19 века.
Вот так он выглядел:

Жозеф Луи Гей-Люссак являлся последователем ученого Клода Луи Бертолле, химика французского происхождения. С начала 19 века он преподавал химические науки в одном из университетов Франции, а также преподавал физические науки в одном из самых известных институтов Европы — Сорбонне.
С 30-х годов 19 века преподавал химические науки в Парижском ботаническом саду. Также в это время он занимался депутатскими делами — продвигал и поддерживал науку во Франции. Более сорока лет занимался редакторской работой вместе с другим французским ученым Франсуа Араго в журнале о науке «Анализы химии и физики». Активно занимался вопросами науки в государстве — работал на высоких должностях, поддерживал научных работников Франции того времени. Был также одним из немногих почетных представителей из иностранного государства в рядах Петербургской научной академии. Жозеф Луи Гей-Люссак по праву считается одним из самых значимых ученых во всей французской истории. Имя этого человека занесено в перечень самых великих ученых во Франции.
Свои эксперименты в области веществ в газовом состоянии он начал в начале 19 века. Он наблюдал за поведением газов в различных условиях: как они ведут себя в разных температурных режимах, как изменяются их состояния, как формируется пар.
Примечание 1
Похожие процессы исследовал и английский ученый Джон Дальтон, в одно время с Гей-Люссаком. Но, как это было в то время, ученые не подозревали об одинаковых экспериментах. Джон Дальтон добился значительных успехов в этой области при помощи сильного оборудования: он доказал, что в процессе преобразования температурных режимов от полного нуля до 100 градусов по Цельсию воздушный объем станет больше примерно на 0,302. Ученым до него удавалось выяснить только, что увеличивается объем на 0,38.
Так выглядел Джон Дальтон:
В начале 19 века Жозеф Луи Гей-Люссак совершил более точные измерения своего исследования, в результате он получил показатель в 0,375. Именно этот показатель многие годы применяли к своим вычислениями именитые физики в Европе. Согласно современным показателям, данное значение эквивалентно температурному режиму, который характерен для полного нуля, то есть -266,7 градусов по Цельсию.
После проведения похожих исследований с различными веществами в газовом состоянии, французский ученый вывел, что данный показатель является одинаковым для всяких газовых веществ на планете. Причем это утверждение идет в разрез с научным мнением, что различные газовые вещества увеличиваются в объеме в процессе увеличения температуры по-разному.
То есть в науке предпочитают использовать мнение о том, что газы могут меняться по одному параметру по-разному.
Формулы, графики, уравнение
Представим несколько графиков изобарного процесса. График для изобарного процесса обычно в физике носит название «изобара». Посмотрите на график ниже: на VT находится графическое изображение изобара ([V=consttimes]) , представляет собой прямую на графике.
Посмотрите на диаграмму зависимости:
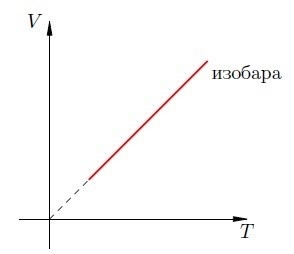
Обратите внимание, что пунктир на графическом представлении является отображением того, что, если применять то же самое для настоящего газового вещества в условиях очень низких температурных режимов прототип идеального газа, на котором основана теория Гей-Люссака, не будет верен. Получается, что в случае понижения температурного режима газовые частицы начинают совершать меньше движения, тогда силы взаимовлияния между молекулами начинают сильнее воздействовать на процессы передвижения. К примеру, всем понятно, что мяч, который летит медленно, поймать гораздо легче, чем мяч, который летит быстро. Получается, что при критически низких температурных режимах газовые вещества становятся жидкими веществами.
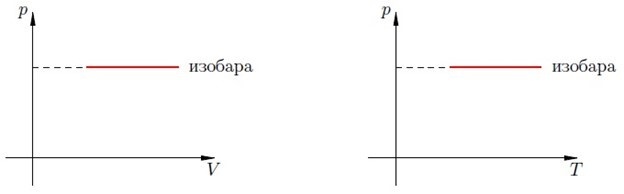
Что будет, если поменять давление? В результате подобного эксперимента получится, что изобара будет стремиться становиться ниже по мере увеличения показателей давления. Для того, чтобы понять, как это работает, необходимо исследовать два типа изобар, у которых различные показатели давления, то есть давление ([p_]) и ([p_]) .

Предположим, что температурные показатели не изменяются. Получится, что ([V_]) . Однако согласно физическому закону Бойля-Мариотта получится, что в случае постоянства температурного режима объем будет уменьшаться по мере увеличения давления. Получается, что ([p_>p_]) .
В данной системе изобара представляет собой прямую, которая перпендикулярна оси p:
Количество теплоты при изобарном процессе
Существует несколько вариаций выделения теплоты в изобарном процессе. Если наблюдается изобарное расширение, тогда получится, что Q>0, потому что теплота воспринимается газовым веществом, а газовое вещество производит работу с положительным знаком. В случае изобарного сжатия получится, что Q]) . Энергия изнутри уменьшается, тогда U
Примеры
Примеры изобарного процесса можно найти даже в быту. Например, изобарным процессом является увеличение температуры воды, когда та находится в открытом для источника тепла сосуде.
Также примером изобарного процесса может служить увеличение объемов газового вещества внутри цилиндра, у которого вольно ходящий поршень. В двух примерах, которые были нами приведены, наблюдается эквивалентность показателей давления показателям давления атмосферного.
В том случае, когда изобарный процесс протекает слишком долго, показатели давления в подобной системе можно принять за неизменяемые, эквивалентные внешним показателям давления; температурный режим изменяется также слишком долго, во всех временных промежутках остается справедливым термодинамическое равновесие, тогда можно говорить об обратимости изобарного процесса.изобарный процесс
Насколько полезной была для вас статья?
Изохорный процесс: формула, графики, уравнения
В термодинамике существует несколько типов процессов, которые могут происходить в условиях, когда масса (m) газов (которые рассматриваются как физический объект для этих исследований) всегда остается постоянной, но иные параметры состояния могут изменяться. Параметры состояния включают давление, объем, температуру и энтропию. Так, в зависимости от того, какой параметр системы сохраняется неизменным, в ходе этого процесса я разделяю четыре их типа: 1) изотермический процесс (низкая или высокая температура сохраняется постоянной), 2) изобарный процесс (разное давление сохраняется постоянным во время всего процесса, выполняемого с системой), 3) изохорный (объем удерживают постоянным на протяжении всего процесса) и 4) адиабатический (постоянная энтропия, то есть отсутствует обмен со средой вокруг физического процесса ни теплом, ни веществом).
Изохорный процесс — это процесс видимого изменения разного состояния в рабочей термодинамической системе видимых тел, значимый процесс идет при держании его в постоянном объеме (V=const).
Макроскопические тела — это тeла, которые рассматриваются в определении изохорного процесса, обычно включают газы и жидкости. Так, для таких макроскопических тел, если необходимо проводить процесс изохорно, то необходимо нагревать/охлаждать или изменять давление, но при этом соблюдать условие — объем должен оставаться неизменным.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Кто открыл изохорный процесс
Первым, кто проводил испытания над идеальным газом, который использовался как модельная система, при этом были созданы условия в системе, чтобы объем газа оставался постоянны, был французский физик Гийом Амонтон. Первые испытания в такой системе, которые он проводил, были опубликованы им в 1702 году в «Парижских мемуарах». В этой работе были указаны условия проведения данного эксперимента, то есть модель — это идеальный газ, были соблюдены условия, чтобы его объем не менялся, а также важным условием было то, что система была помещена в «стабильный воздушный термометр». В ходе своего эксперимента Амонтон заметил, что при стабильном нагревании давление газа увеличивалось с увеличением T (пропорционально), а жидкость по чуть-чуть вытеснялась веществом в газовой форме и переходила в идущую дальше выступающую колонну, заполняя ее.
Изучение важного для науки изохорного процесса не остановилось на экспериментах Амонтона, его будущее предопределил физик из Англии — Джон Дальтон в 1801 году. Он провел ряд экспериментов, с помощью них удалось выяснить, что при одних и тех же начальных и конечных, т.е. при стабильных давлениях, при варьировании температуры газы сжимаются/расширяются. Третьим важным этапом в изучении интересного изохорного процесса стало овладевание этм процессом французским физиком Жозефом Луи Гей-Люссаком. Он провел собственное независимое исследование, в результате которого эксперименты Далтона ознаменовались как подтвержденыt. А позже Гей-Люссак смог объединить свои выводы с уже известным зависимостью Бойля–Мариотта, именно в результате этой комбинации был подробнейшим образом описан изохорный процесс, где модельной системой является идеальный газ. А правило, описывающее зависимости V газа от T для изохорного процесса было названо в честь исследователя, то есть вторым законом Гей-Люссака. Иное название «закон Шарля» ему дал экспериментатор, приложивший руку к открытию этого уложения, а именно в 1787 году Шарль с помощью эксперимента проверил зависимость давления газа от температуры при поддержании в системе одинакового объема газа, и только после этого в 1802 году Гей-Люссак дополнил этот закон термодинамики.
Условия протекания изохорного процесса
Первым и наиболее важным для реализации процесса — это нахождение ТД системы в замкнутой системе (сосуде или пространстве), чтобы объем в течение всего процесса оставался неизменным. Второе — исследуемое вещество должно находиться в закрытой системе, чтобы не было обмена системы веществом или теплом с окружающей средой (воздухом и т.д.) для простого описания процесса, а также для разработки и вывода более корректных данных. Третьим условием, важным для того, чтобы поток обрабатывался при V = const, является постепенное изменение (повышение/ понижение) градуса в системе.
Формулы, графики, уравнения
Закон Шарля (второй закон Гей-Люссака). Давления интересующего газа постоянной массы при соблюдении постоянного (const) исследованного объема прямо пропорционально температуре газа.
(pV;=;frac mMRT;=;nRT) , где m — масса газа(кг), M — молекулярная масса газа(кг/моль), R = 8,314 Дж/(моль*К) — универсальная газовая постоянная, T — температура (К), n — количество молей газа.
Что означает тоже самое, что
То есть отношение давления к температурев ходе всего процесса остается неизменяемым.
Исходя из того факта, что для изопроцессов с постоянным объемом давление газа в системе прямо пропорционально температуре, то эту зависимость можно представить на графиках для представления. Более того, принято строить графики в разных координатах переменных параметров состояния (давления, температуры и объема), следовательно, существует три типа графиков в разных координатах: p-V, p-T и V-T (рис.1). На любом из этих графиков объем лишается возможным меняться, потому что мы рассматриваем изохорный процесс, а линия графика зависимости называется изохорой.
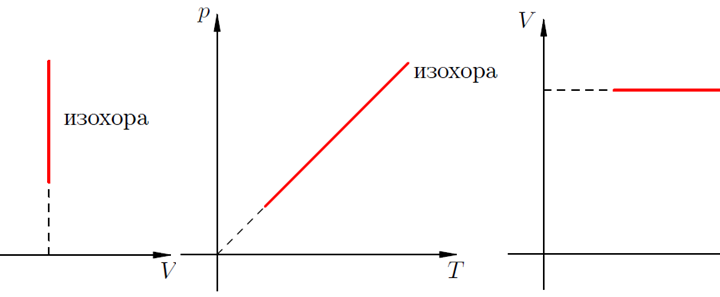
Рис.1. Графики зависимостей для изохорного процесса в различных координатах.
Количество теплоты при изохорном процессе
Определяется из I Закона ТД, который звучит следующим образом (пока что без наложения условия, что объем газа неизменный), а также при условии, что работу делает сама система, а не внешние силы над системой:
Количество теплоты, полученное системой, расходуется на изменение внутренней энергии и совершения системой работы над внешними силами (телами и т.д.)
(triangle U= Q — A )
Когда мы работаем в системе с стабильным объемом, то есть протекает изохорный процесс, то I начало термодинамики приобретает некоторые ограничения, первое из которых — это то, что работа, которую совершает система в изохорном процессе, будет равна нулю:
Таким образом, работа в ходе изопроцесса с постоянным объемом не совершает работы.
Тогда количество теплоты, которое мы определяли по I закон термодинамике будет равно только чувствительным колебаниям внутренней энергии системы:
Внутренняя энергия при изохорном процессе
Варьирование внутренней энергии — это разница между значениями начальной уникальной внутренней энергии системы и конечной важной. То есть однажды при начальной температуре системы и при якобы конечной температуре у нас будут два разных значения внутренней энергии, откуда мы получим формулу: (triangle U;=U(T_2)-U(T_1)=;Q;)
Откуда еще раз видно, что количество тепла системы в изохорном процессе будет определяться только изменением внутренней энергии системы, а именно ее начального и конечного состояний.
Примеры
Цикл Отто — это процедура физической стороны, в которой действуют законы термодинамики. В ней описываются манипуляции всего процесса, который выполняет двигатель внутреннего сгорания (ДВС) с воспламенением и последующим воспламенением сжатой смеси от стороннего источника энергии – это цикл, по которому работают все бензиновые двигатели.
Теоретически немецкий инженер То, работая над этим циклом, создал идеальные условия, при которых цикл состоит из четырех этапов — процессов, показанных на рисунке 2:
1-2 стадия адиабатического сжатия рабочего тела
2-3 стадия изохорной подачи тепла к рабочему телу
3-4 стадия адиабатического расширения тела
4-1 стадия охлаждения рабочего тела при постоянном объеме
Также изохорный процесс часто используют для решения физических задач, используя для этого модельные системы. Рассмотрим несколько задач, где используется перводокакзанный закон термодинамики и закон Шарля.
Вещество в газовой форме располагается в баллоне при температуре 400 К. До какой температуры нужно разогреть газ, чтобы его давление выросло в 1,5 раза?
Так как разогрев газа по условиям данным нам в задачи идёт при постоянном объеме, значит перед нами изохорный процесс.
При изохорном процессе:
Определите количество теплоты, которое нужно затратить на нагрев 8,5 г аммиака от 25 до 40 (<>^circ С) при постоянном объеме.
Аммиак имеет следующую химическую формулу — NH_3. С помощью таблицы Менделеева рассчитаем его молекулярную массу:
Количество теплоты, которое система получает при стабильном объеме, то есть в ходе изохорного процесса (по условию), можно рассчитать следующим образом:
(Q_p=nast C_vasttriangle T=nast C_vast(T_2-T_1);=;fracast C_vast(T_2-T_1).)
Для определения C_v –теплоемкости газа необходимо вспомнить, что аммиак — это химическое вещество, геометрия которого — треугольная пирамида. Таким образом, молекулярная теплоемкость идеального газа для изохорного процесса без учета колебательных степеней свободы (потому что низкие температуры, и они заморожены) для нелинейной многоатомной молекулы будет равно:
Подставляем все известные значения в формулу нахождения количества теплоты и находим ее значение:
Ответ: 187 Дж теплоты будет затрачено системой на нагрев от 25 до 40 (<>^circ С) при постоянном объеме.
https://wiki.fastfine.me/fizika/izobarnyj-process